电路中的阻抗计算使用复数是因为电路中存在电阻、电感和电容等元件,这些元件在交流电路中的行为会产生相位差。复数表示具有大小和方向的矢量,能够方便地描述交流电的相位和幅值,从而更准确地计算电路的阻抗。在交流电路分析中,使用复数进行阻抗计算是必要的。
本文目录导读:
在电路分析中,阻抗是一个非常重要的物理量,它描述了电路对交流信号的阻碍作用,阻抗的计算涉及到交流电路中的电压和电流,而在交流电路中,电压和电流都是随时间变化的,为了准确描述这种变化并计算阻抗,我们需要引入复数的概念,本文将探讨为什么电路的阻抗计算中用到了数学中的复数,并阐述复数在电路分析中的重要作用。
交流电路的基本特性
在交流电路中,电压和电流都是随时间变化的,这种变化导致了电路中的相位差异,使得电压和电流之间的关系变得复杂,为了描述这种关系,我们需要引入复数,复数的引入使得我们可以同时描述电压和电流的幅度(大小)和相位(角度),从而更准确地描述交流电路的特性。
复数的定义及基本性质
复数是由实数和虚数组成的数,一般表示为z=a+bi(其中a为实部,b为虚部,i为虚数单位),在复数中,我们可以进行加、减、乘、除等运算,复数具有许多独特的性质,如乘法满足分配律等,这些性质使得复数在电路分析中具有重要的应用价值。
复数在电路阻抗计算中的应用
1、阻抗的定义
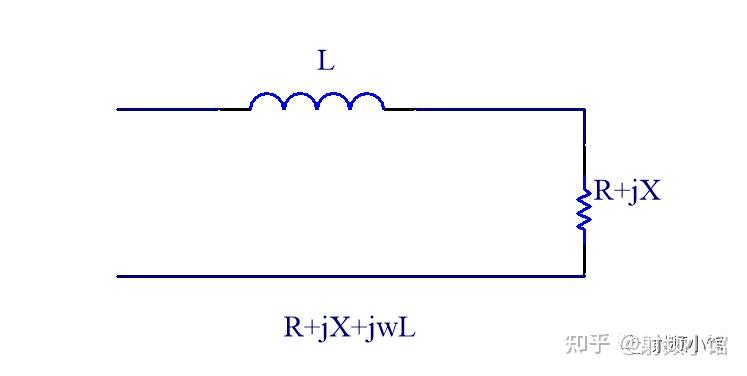
阻抗是交流电路中电压与电流之比,它描述了电路对交流信号的阻碍作用,在交流电路中,阻抗是一个复数,包含了电阻、电感和电容的影响。
2、复数在阻抗计算中的必要性
由于交流电路中的电压和电流是随时间变化的,因此阻抗也会随时间变化,为了准确描述这种变化,我们需要引入复数的概念,通过复数,我们可以同时描述阻抗的幅度和相位,从而更准确地计算电路的阻抗。
3、复数在阻抗计算中的具体作用
(1)描述相位差:复数中的虚部可以表示电压和电流之间的相位差,这对于计算交流电路的阻抗非常重要。
(2)简化计算:通过复数的运算,我们可以简化交流电路中的阻抗计算,使得计算过程更加简洁和高效。
(3)分析电路特性:复数可以帮助我们分析交流电路的频率响应、谐振等特性,从而更好地理解电路的性能。
复数在电路分析中的其他应用
除了阻抗计算外,复数在电路分析中还有其他重要的应用,如:
1、分析正弦稳态交流电路:通过复数表示电压和电流,可以方便地分析正弦稳态交流电路的特性。
2、求解线性时不变微分方程的解:在电路分析中,许多问题可以转化为线性时不变微分方程,通过复数的运算,可以方便地求解这些方程的解。
3、频率域分析:在频率域分析中,复数可以帮助我们分析电路的频响特性,从而了解电路在不同频率下的性能。
本文探讨了为什么电路的阻抗计算中用到了数学中的复数,并阐述了复数在电路分析中的重要作用,通过引入复数的概念,我们可以更准确地描述交流电路的特性,简化阻抗计算,并分析电路的频率响应和其他性能,复数是电路分析中不可或缺的数学工具。
展望
随着电力电子技术和通信技术的不断发展,复数在电路分析中的应用将越来越广泛,我们将需要更加深入地研究复数的性质及其在电路分析中的应用,以更好地解决实际应用中的问题,随着计算机技术的不断进步,复数运算的自动化程度将不断提高,使得复数在电路分析中的应用更加便捷和高效,复数将继续在电路分析中发挥着重要的作用,为我们解决复杂的电路问题提供有力的支持。

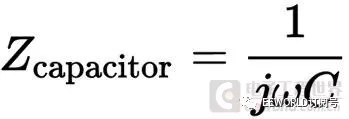
 京ICP备11000001号
京ICP备11000001号